Diffusion models for time-series forecasting

Introduction

Diffusion models have taken the world by storm over the past few years, showcasing impressive capabilities particularly in the field of image generation, with this perhaps becoming their most renowned application. These models have unique characteristics that make them suitable for image generation, however there are more domains where they can be used, with one such being time series forecasting. This potential prompted a deeper investigation through a master’s thesis written in collaboration with Modulai.

Diffusion models

In essence, diffusion models are trained by incrementally adding noise to a data point, effectively blurring and distorting the original data (shown in the figure below). The model then learns a reverse process, known as denoising. Through this process, the model aims to grasp the correct statistical distribution of the data, which is later utilized when sampling to generate results. The critical point here is that the model doesn’t return a single expectation value but rather a stochastically generated sample from a learned distribution. This makes it particularly well-suited for performing time series forecasting on datasets with complex correlations.

Let us have a look at a simple example of why this is useful. The graph below showcases samples generated from a bimodal distribution. As can be seen, the expectation value of this distribution is one that is highly unlikely to be sampled.

In many widely used forecasting models, the model is trained to output some sort of expectation value which can be troublesome if the underlying data has complex distributions. Thanks to diffusion models being tasked with understanding the underlying distribution, they may generate more realistic and probable forecasts. Bimodal and other complex distributions like these are not merely theoretical constructs; they are often encountered in real-world scenarios.

Another significant advantage of diffusion models is that their output is inherently probabilistic due to the sampling process, meaning the model outputs slightly different forecasts each time it is run. This variance can be interpreted as the model’s uncertainty. In other words, in situations that are more challenging to forecast, the model may exhibit a higher degree of uncertainty providing further valuable insights. The figure below showcases some examples of forecasts and the associated uncertainty, with the light green region visualizing the variance for each forecast.

We did observe a correlation between the samples variance, and the error indicating that there exists information in the uncertainty signal.

The forecasting task

A versatile architecture capable of forecasting large-scale time series problems with both spatial and temporal correlations was sought to be developed. Examples of such problems include traffic flow forecasting, weather condition forecasting, and power grid forecasting. Therefore, the American power grid was chosen as a suitable forecasting challenge to develop a diffusion based architecture around. The dataset consisted of power data from 67 nodes across the United States. The following hourly data was provided for each node;

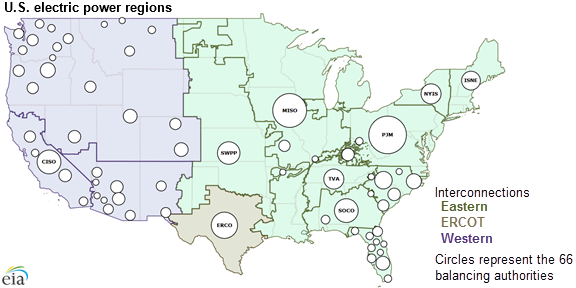
The model’s task was to forecast the state of the power grid, hour by hour, 72 hours into the future using a rollout method. Covariates, data points that are not to be forecasted but are there to assist the model, was also provided to the model. The covariate data consisted of financial data such as currency prices, and weather data. The figure below illustrates the relative size in terms of power usage, and location of these balancing authorities across the country.

Graph representation

Given that we are forecasting a proper physical system spread out across the US, the dataset will have mainly spatial and temporal correlations. Temporal correlations capture patterns and dependencies over time, reflecting how the state of the system evolves from one hour to the next. Spatial correlations, on the other hand, capture the interdependencies between different locations within the power grid. These correlations are essential for understanding how changes or anomalies at one node can affect others across the network.

To effectively model these spatial correlations, we used a graph structure. In this structure, each node represents a node within the power grid, and edges between nodes represent the connections between the balancing authorities (i.e. nodes that can send power between each other). This graph-based approach allows us to help the model understand where correlations exist, decreasing the amount of data that would otherwise be needed for the model to identify them. We then create a sequence of graphs, with each graph representing the state of the power grid for one corresponding hour. We then feed this sequence of graphs to a diffusion block where the diffusion process takes place.

An overview of the architecture can be seen in the figure above, which illustrates the process flow and the components used in our approach:

The architecture begins with historical power data formatted as a sequence of graphs, which is processed using a Graph Attention Network (GAT) to capture spatial correlations effectively. This processed data is then fed into a Long Short-Term Memory (LSTM) network to handle temporal correlations. Concurrently, covariate data, representing additional relevant features, is divided into local and global categories. Both categories are processed using another GAT to integrate the covariates with the graph data. The outputs of the LSTM and covariate GATs are then combined and passed through a diffusion block, which is where the diffusion takes place. Finally, the output of the diffusion block generates a denoising vector, which is used when performing de-noising.

This approach ensures that both spatial and temporal correlations are accurately captured, providing a robust model for performing time-series forecasting.

Comparisons to other models

After speaking with industry experts within the field of energy forecasting, our understanding is that gradient boosted decision trees (GBDT) are commonplace. This prompted an in depth comparison between the diffusion model and XGBoost, a widely used GBDT model. The diffusion model consistently outperforms XGBoost across all features, apart from the first ~2 hours of the forecast. This can be seen in the plot below which showcases the average absolute error of XGBoost and the diffusion model. When the number is larger than 0, diffusion outperforms XGBoost. When looking at this chart, bear in mind that the reason for the difference relative size of the errors across features is that they are not normalized.

Outlook

In conclusion, this thesis project demonstrates that diffusion models are a viable architecture for time series forecasting, showcasing their strong performance. While it is often challenging in machine learning to pinpoint precisely why a model performs well, one hypothesis is that diffusion models excel at capturing multi-modal and complex correlations that simpler regression models struggle with. As research continues, the potential and effectiveness of diffusion models in time series forecasting appear increasingly promising, paving the way for more accurate and reliable predictive analytics.